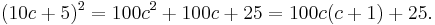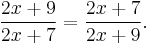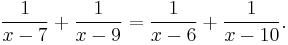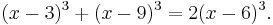Bharati Krishna Tirtha's Vedic mathematics
- for the actual mathematics of the Vedic period, see the articles on Sulba Sūtras and Indian mathematics.
Vedic mathematics is a system of mathematics consisting of a list of 16 basic sūtras, or aphorisms. They were presented by a Hindu scholar and mathematician, Bharati Krishna Tirthaji Maharaja, during the early part of the 20th century.[1]
Tirthaji claimed that he found the sūtras after years of studying the Vedas, a set of sacred ancient Hindu texts.[2] However, Vedas do not contain any of the "Vedic mathematics" sutras.[3][4]
The calculation strategies provided by Vedic mathematics are said to be creative and useful, and can be applied in a number of ways to calculation methods in arithmetic and algebra, most notably within the education system. Some of its methods share similarities with the Trachtenberg system.
Contents
|
Origin of the system
There has been much controversy among Indian scholars about Tirthaji’s claims that the mathematics is Vedic and that it encompasses all aspects of mathematics (Kansara, 2000).
First, Tirthaji’s description of the mathematics as Vedic is most commonly criticised on the basis that, thus far, none of the sūtras can be found in any extant Vedic literature (Williams, 2000). When challenged by Prof K.S. Shukla to point out the sutras in question in the Parishishta of the Atharvaveda, Shukla reported that the swamiji said that the sixteen sutras were not in the standard editions of the Parishishta, and that they occurred in his own Parishishta and not any other.[5][6] Considering the lack of references to the sūtras, coupled with the fact that the language style does not seem Vedic, some propose that the sūtras were simply composed by Tirthaji himself
Critics have questioned whether this subject deserves the name Vedic or indeed mathematics. They point to the lack of evidence of any sutras from the Vedic period consistent with the system, the inconsistency between the topics addressed by the system (such as decimal fractions) and the known mathematics of early India, the substantial extrapolations from a few words of a sūtra to complex arithmetic strategies, and the restriction of applications to convenient, special cases. They further say that such arithmetic as is sped up by application of the sūtras can be performed on a computer or calculator anyway, making their knowledge rather irrelevant in the modern world.[7]
In response to criticisms that the sūtras cannot be located within the texts, several people have explained how textual references should not be the basis for evaluating the Vedicity of the mathematics (Agrawala, 1992). Some propose that Vedic mathematics is different from other scientific work because it is not pragmatically worked out, but is based on a direct revelation, or an “intuitional visualisation” of fundamental mathematical truths (Agrawala, 1992; Pratyagatmananda, 1965). Tirthaji has been described as having the same “reverential approach” towards the Vedas as the ancient rishis that formed them. Thus, it seems as though some believe that Tirthaji may not have found the sūtras within the Vedas, but that he received them spiritually as the rishis did, which should validate them as Vedic. The controversy about the Vedicity of the mathematics is further confused by the double meaning of veda. Since veda can be translated to mean ‘knowledge’, it is also possible that Vedic mathematics simply refers to the fact that the sūtras are supposed to present all knowledge of mathematics. Tirthaji’s definition of veda does not clearly clarify whether he uses it to represent ‘all knowledge’ or the Vedic texts; rather, it seems that he uses it to refer to both. His more recent book titled 'Vedic Mathematics' can be purchased locally.
The sūtras (formulae or aphorisms)
Vedic mathematics is based on sixteen sūtras which serve as somewhat cryptic instructions for dealing with different mathematical problems. Below is a list of the sūtras, translated from Sanskrit into English:
- "By one more than the previous one" [8]
- "All from 9 and the last from 10"[9]
- "Vertically and crosswise (multiplications)"[10]
- "Transpose and apply"[11]
- "Transpose and adjust (the coefficient)"[12]
- "If the Samuccaya is the same (on both sides of the equation, then) that Samuccaya is (equal to) zero"[13][14]
- By the Parāvartya rule [15][16]
- "If one is in ratio, the other one is zero." [17]
- "By addition and by subtraction."[18]
- By the completion or non-completion (of the square, the cube, the fourth power, etc.)[19][20]
- Differential calculus [21][22]
- By the deficiency
- Specific and general
- The remainders by the last digit
- "The ultimate (binomial) and twice the penultimate (binomial) (equals zero),"[23]
- "Only the last terms,"[24][25][26][27]
- By one less than the one before
- The product of the sum
- All the multipliers
Subsūtras or corollaries
- "Proportionately"[28]
- The remainder remains constant
- "The first by the first and the last by the last" [29]
- For 7 the multiplicand is 143
- By osculation
- Lessen by the deficiency
- "Whatever the extent of its deficiency, lessen it still further to that very extent; and also set up the square (of the deficiency)".[30]
- "By one more than the previous one"[31]
- "Last totaling ten"[32][33]
- The sum of the products
- "By (alternative) elimination and retention (of the highest and lowest powers)"[34]
- By mere observation,[35][36]
- The product of the sum is the sum of the products
- On the flag
Editor's list of 16 Sūtras and 13 Sub-sūtras or corollaries from the Vedas[37]
To check the factorization of polynomial expressions: "The product of the sum of the coefficients (SC) in the factors is equal to the sum of the coefficients in the product." The SC of the product (the expression) = Product of the SC (in the factors). Additionally, this sub-sūtra helps to fill in the gaps when some factors are known.[38]
Background information on the Vedas
The word “veda” has two basic meanings. The first, a literal translation of the Sanskrit word, is “knowledge” (Veda). The second, and most common meaning of the word, refers to the sacred ancient literature of Hinduism, the Vedas, a collection of hymns, poetry and Hindu ceremonial formulae (Veda). Believed to be one of the oldest human written records, the Vedas date back over 4000 years (Gaskell, 2000). Traditionally, they were passed down orally and adapted from generation to generation by sacred sages called rishis, before eventually emerging written in Vedic, an ancient form of Sanskrit.
The Vedas are divided into four main sections: the Rig-veda, Sama-veda, Yajur-veda and the Atharva-veda, known collectively as the Samhitas (Veda). The first three, the Rig-veda, Sama-veda, and Yajur-veda are basically ritual handbooks that were used by priests during the Vedic period (1500–500 BCE) (Veda). Vedic mathematics is apparently part of the fourth Veda, Atharva-veda, which is distinct from the others in several ways. First, unlike the religious focus of the other Vedas, the Atharva-veda contains hymns, spells and magical incantations for personal and domestic use (Veda). Also, the Atharva-veda, which was written later than the other Vedas, was not always considered authoritative, but only became so after being accepted by the Brahmans, the highest order of Hindu priests (Veda). Collectively, the Vedas include information about a huge range of subjects, spanning religion, medicine, architecture, astronomy, etc. (Gaskell, 2000).
Although there is controversy about whether the Vedas themselves actually include references to mathematics, the roots of sophisticated mathematics have actually been traced back to the Vedic era. Ancient Indian Vedic civilizations are known for being skilled in geometry, algebra and computational mathematics complex enough to incorporate things like irrational numbers (Dutta, 2002). Furthermore, all ancient Indian mathematics literature is composed completely in verse; there was a tradition of composing terse sūtras, like those of Vedic mathematics, to ensure that information would be preserved even if written records were damaged or lost (Dutta, 2002).
Methods described in the sūtras
It is not difficult to understand and apply the Vedic mathematical strategies, as long as one does not rely on the sūtras alone for mathematical insight. Those studying Vedic mathematics tend to strongly rely on the examples and explanations Tirthaji provides in his book.
All from nine and the last from ten
When subtracting from a large power of ten with many columns of zeros, it is not necessary to write the notation for "borrowing" from the column on the left. One can instead subtract the last (rightmost) digit from 10 and each other digit from 9. For example, when one is subtracting ten thousand minus 4,679, the leftmost three digits of 4,679—4, 6 and 7--are subtracted from 9, and the rightmost nonzero digit—that is, 9--is subtracted from 10, yielding the solution: 5,321. This method is also used when finding the deficit from the next larger power of ten when setting up a multiplication problem using the "cross-subtraction" method.[39]
First corollary, when squaring numbers
"Whatever the extent of its deficiency, lessen it still further to that very extent; and also set up the square (of that deficiency)"[40]
For instance, in computing the square of 9 we go through the following steps:
- The nearest power of 10 to 9 is 10. Therefore, let us take 10 as our base.
- Since 9 is 1 less than 10, decrease it by the deficiency (9 - 1 = 8). This is the leftmost digit of our answer.
- On the right hand side put the square of the deficiency, which is 1². Hence, the square of nine is 81.
Similarly, 8² = 64, 7² = 49, 6²=36.
For numbers above 10, instead of looking at the deficit we look at the surplus. For example:
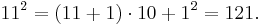
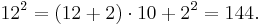
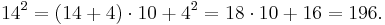
![25^2 = [(25%2B5)\cdot 2]\cdot 10%2B5^2 = 625.\,](/2012-wikipedia_en_all_nopic_01_2012/I/32b7f58b27b7f4899be09f857e6aa834.png)
![35^2 = [(35%2B5)\cdot 3]\cdot 10%2B5^2 = 40\cdot3\cdot10%2B25 = 1225.\,](/2012-wikipedia_en_all_nopic_01_2012/I/e65c0e97bef652dd22d1aa6b2b017a6c.png)
- and so on.
This method of squaring is based on the fact that 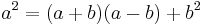 [41] where a is the number whose square is to be found and b is the deficit (or surplus) from nearest product of 10.
[41] where a is the number whose square is to be found and b is the deficit (or surplus) from nearest product of 10.
By one more than the one before
"Ekādhikena Pūrveṇa" is the Sanskrit term for "[by] One more than the previous one". It provides a simple way of calculating values like 1/x9 (e.g.: 1/19, 1/29, etc.). The sūtra can be used for multiplying as well as dividing algorithms.
For example, to calculate 1/19, x = 1 . For the multiplication algorithm (working from right to left), the method is to start by denoting the dividend, 1, as the first (rightmost) digit of the result. Then that digit is multiplied by 2 (i.e.: x + 1 ), and noted to that next digit to its left. If the result of this multiplication was greater than 10, (value – 10) is noted, and the "1" is noted as a carry which will be added to the next digit directly after multiplying.
The preposition "by" means the operations this formula concerns are either multiplication or division. [In case of addition/subtraction preposition "to" or "from" is used.] Thus this formula is used for either multiplication or division. It turns out that it is applicable in both operations.
Note: This sūtra can also be applied to multiplication of numbers with the same first digit and the sum of their last unit digits is 10.
An interesting sub-application of this formula is in computing squares of numbers ending in five. Examples:
- 35×35 = ((3×3)+3),25 = 12,25 and 125×125 = ((12×12)+12),25 = 156,25
or by the sūtra, multiply "by one more than the previous one."
- 35×35 = ((3×4),25 = 12,25 and 125×125 = ((12×13),25 = 156,25
The latter portion is multiplied by itself (5 by 5) and the previous portion is square of first digit or first two digit (3×3) or (12×12) and adding the same digit in that figure (3or12) resulting in the answer 1225.
(Proof) This is a simple application of 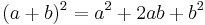 when
when 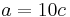 and
and 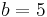 , i.e.
, i.e.
It can also be applied in multiplications when the last digit is not 5 but the sum of the last digits is the base (10) and the previous parts are the same. Examples:
- 37 × 33 = (3 × 4),7 × 3 = 12,21
- 29 × 21 = (2 × 3),9 × 1 = 6,09 ?
This uses 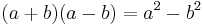 twice combined with the previous result to produce:
twice combined with the previous result to produce:
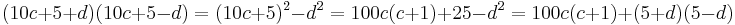 .
.
We illustrate this sūtra by its application to conversion of fractions into their equivalent decimal form. Consider fraction 1/19. Using this formula, this can be converted into a decimal form in a single step. This can be done by applying the formula for either a multiplication or division operation, thus yielding two methods.
Method 1: example: using multiplication to calculate 1/19
For 1/19, since 19 is not divisible by 2 or 5, the fractional result is a purely circulating decimal. (If the denominator contains only factors 2 and 5, the result is a purely non-circulating decimal, else it is a mixture of the two: a short non-circulating sequence of digits, followed by an endless repetition.) Each factor of 2 or 5 or 10 in the denominator gives one fixed decimal digit.
So we start with the last digit of the result, being the dividend:
- 1
Multiply this by "one more", that is, 2 (this is the "key" digit from 'Ekādhikena')
- 21
Multiplying 2 by 2, followed by multiplying 4 by 2
- 421 → 8421
Now, multiplying 8 by 2, sixteen
- 68421
- 1 ← carry
multiplying 6 by 2 is 12 plus 1 carry gives 13
- 368421
- 1 ← carry
Continuing
- 7368421 → 47368421 → 947368421
- 1
Now we have 9 digits of the answer. There are a total of 18 digits (= denominator − 1) in the answer computed by complementing the lower half (with its complement from nine):
- 052631578
- 947368421
Thus the result is 1/19 = 0.052631578,947368421 repeating.
1
21
421
8421
68421 (carry 1) – we got 16, so we keep 6 and carry 1
368421 (carry 1) – we get 6*2 + carry 1 = 13, so we keep 3 and carry one
do this to eighteen digits (19–1. If you picked up 1/29,
you'll have to do it till 28 digits). You'll get the following
1/19 = 052631578947368421
10100111101011000
Run this on your favorite calculator and check the result!
Method 2: example: using division to calculate 1/19
The earlier process can also be done using division instead of multiplication. We start again with 1 (dividend of "1/x9"), dividing by 2 (" x + 1 "). We divide 1 by 2, answer is 0 with remainder 1
- result .0
Next 10 divided by 2 is five
- .05
Next 5 divided by 2 is 2 with remainder 1
- .052
next 12 (remainder,2) divided by 2 is 6
- .0526
and so on.
Other fractions can sometimes be converted into the format of "d/x9"; as another example, consider 1/7, this is the same as 7/49 which has 9 as the last digit of the denominator. The previous digit is 4, by one more is 5. So we multiply (or divide) by 5, that is:
…7 → 57 → 857 → 2857 → 42857 → 142857 → .142,857 (stop after 7 − 1 digits)
3 2 4 1 2
Multiplying by 11
11×35= 385
- (1) The five in the ones place of the answer is taken from the five in 35.
- (2) The eight in the answer is the sum of 35 (3+5=8).
- (3) The three in the hundreds place of the answer is taken from the three in 35.
However, if in step #2 the sum is greater than 9, the sum's left digit is added the first digit of the number multiplied by 11. For example:
11×59= 649
- (1) The nine in the ones place of the answer is taken from the nine in 59.
- (2) The four in the answer is the right digit in the sum of 59 (5+9=14)
- (3) The six in the hundreds place of the answer is taken from the sum of the five in 5'9 and the digit in the tens place from the sum of 59 (5+9=14) --> (5+1=6)
The steps for multiplying a three-digit number by 11 are as follows:
11×768= 8448
- (1) The 8 in the ones place of the answer is taken from the eight in 768.
- (2) The 4 in the tens place of the answer is taken from the sum of 8, in the ones place of 768, and 6, in the tens place of 768 (8+6=14). As 14 is greater than 9, the 1 is carried over to step 3.
- (3) The 4 in the hundreds place of the answer is taken from the sum of 6, in the tens place of 768, and 7, in the hundreds place of 768, plus the carried 1 from step 2 (6+7+1=14). As 14 is greater than 9, the 1 is carried over to step 4.
- (4) The 8 in the thousandths place of the answer is taken from the sum of 7, in the hundreds place of 768, plus the carried 1 from step 3 (7+1=8).
Vertically and crosswise
This formula applies to all cases of multiplication and is very useful in division of one large number by another large number.
For example, to multiply 23 by 12:
2 3
| × |
1 2
2×1 2×2+3×1 3×2
2 7 6
So 23×12=276.
When any of these calculations exceeds 9 then a carry is required.
This is the equivalent of (10a+b)(10c+d)=100ac+10(ad+bc)+bd.
Transpose and apply
This formula complements "all from nine and the last from ten", which is useful in divisions by large numbers. This formula is useful in cases where the divisor consists of small digits. This formula can be used to derive the Horner's process of Synthetic Division.
When the samuccaya is the same, that samuccaya is zero
This formula is useful in solution of several special types of equations that can be solved visually. The word samuccaya has various meanings in different applications. For instance, it may mean a term which occurs as a common factor in all the terms concerned. A simple example is equation "12x + 3x = 4x + 5x". Since "x" occurs as a common factor in all the terms, therefore, x = 0 is a solution. Another meaning may be that samuccaya is a product of independent terms. For instance, in (x + 7) (x + 9) = (x + 3) (x + 21), the samuccaya is 7 × 9 = 3 × 21, therefore, x = 0 is a solution. Another meaning is the sum of the denominators of two fractions having the same numerical numerator, for example: 1/ (2x − 1) + 1/ (3x − 1) = 0 means we may set the denominators equal to zero, 5x – 2 = 0.
Yet another meaning is "combination" or total. This is commonly used. For instance, if the sum of the numerators and the sum of denominators are the same then that sum is zero. Therefore,
Therefore, 4x + 16 = 0 or x = −4.
This meaning ("total") can also be applied in solving quadratic equations. The total meaning can not only imply sum but also subtraction. For instance when given N1/D1 = N2/D2, if N1 + N2 = D1 + D2 (as shown earlier) then this sum is zero. Mental cross multiplication reveals that the resulting equation is quadratic (the coefficients of x² are different on the two sides). So, if N1 − D1 = N2 − D2 then that samuccaya is also zero. This yields the other root of a quadratic equation.
Yet interpretation of "total" is applied in multi-term RHS and LHS. For instance, consider
Here D1 + D2 = D3 + D4 = 2x − 16. Thus x = 8.
There are several other cases where samuccaya can be applied with great versatility. For instance "apparently cubic" or "biquadratic" equations can be easily solved as shown below:
Note that x − 3 + x − 9 = 2 (x − 6). Therefore (x − 6) = 0 or x = 6.
This would not work for the apparently quadratic 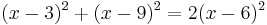 , which has no real or complex solutions.
, which has no real or complex solutions.
Consider
Observe: N1 + D1 = N2 + D2 = 2x + 8. Therefore, x = −4.
This formula has been extended further.
If one is in ratio, the other one is zero
This formula is often used to solve simultaneous linear equations which may involve big numbers. But these equations in special cases can be visually solved because of a certain ratio between the coefficients. Consider the following example:
- 6x + 7y = 8
- 19x + 14y = 16
Here the ratio of coefficients of y is same as that of the constant terms. Therefore, the "other" variable is zero, i.e., x = 0. Hence, mentally, the solution of the equations is x = 0 and y = 8/7.
(alternatively:
- 19x + 14y = 16 is equivalent to:
- (19/2)x +7y = 8.
Thus it is obvious that x has to be zero, no ratio needed, just divide by 2!)
Note that it would not work if both had been "in ratio". For then we have the case of coinciding lines with an infinite number of solutions.:
- 6x + 7y = 8
- 12x + 14y = 16
This formula is easily applicable to more general cases with any number of variables. For instance
- ax + by + cz = a
- bx + cy + az = b
- cx + ay + bz = c
which yields x = 1, y = 0, z = 0.
A corollary says solving "by addition and by subtraction." It is applicable in case of simultaneous linear equations where the x- and y-coefficients are interchanged. For instance:
- 45x − 23y = 113
- 23x − 45y = 91
By addition: 68x − 68 y = 204 → 68 (x − y) = 204 → x − y = 3.
By subtraction: 22x + 22y = 22 → 22 (x + y) = 22 → x + y = 1.
Again, by addition, we eliminate the y-terms: 2x = 4, so x = 2.
Or, by subtraction, we eliminate the x-terms: – 2y = 2, and so y = – 1.
The solution set is {2,-1}. Examples of models which are complete extensions due to j.corcoran and mircea h.orasanu and mircea t.orasanu
Applications
- In the UK, the method is used by teacher Satish Sharma with students in Slough, as well as by Kenneth Williams, teacher, author and spokesman for the Maharishi School in Skelmersdale, Lancashire, both of whom claim that the methods offer significant results for their pupils.[42]
- Multiplier is an integral part of the processor. Vedic multiplier is based on the Vedic mathematics. Vedic multiplier's architecture is based on the Sutra called "Urdhva Tiryakbhyam". Urdhva Tiryakbhyam (Vertically and Crosswise), deals with the multiplication of numbers. This Sutra has been traditionally used for the multiplication of two numbers in the decimal number system. By applying the algorithm to the binary number system, architecture for multiplier is designed. Other sutra used for Vedic multiplier is Nikhilam Sutra which literally means “all from 9 and last from 10”. Although it is applicable to all cases of multiplication, it is more efficient when the numbers involved are large. Compared with the other multipliers, Vedic multiplier has less delay time. [43][44][45] Vedic multiplier is also used for computing Fast Fourier transform.[46]
See also
Notes
- ^ (Trivedi, 1965)
- ^ (Agrawala, 1992)
- ^ Myths and reality : On ‘Vedic mathematics’. S.G. Dani. School of Mathematics, Tata Institute of Fundamental Research. Frontline, 22 October and 5 November 1993.
- ^ The Fraud of Vedic Maths. Hartosh Singh Bal. Open Magazine. 14 August 2010.
- ^ K.S. Shukla, Vedic mathematics — the illusive title of Swamiji’s book, Mathematical Education, Vol 5: No. 3, January–March 1989
- ^ K.S. Shukla, Mathematics — The Deceptive Title of Swamiji’s Book, in Issues in Vedic Mathematics, (ed: H.C.Khare), Rashtriya Veda Vidya Prakashan and Motilal Banarasidass Publ., 1991.
- ^ S.G. Dani Myths and reality: On 'Vedic mathematics'
- ^ Ekādhikena Pūrvena, Vedic Mathematics, Pages 2–12, "By" in the sūtra means that the prescribed arithmetical operation is either multiplication or division. Both are implied since we may proceed leftward and multiply (and carry-over the excess value to the next leftward column) or we may go rightward and divide (while prefixing the remainder). When dividing by a nine's family denominator, the digit to the left of the nine (previous) is increased by one to obtain the multiplier.
- ^ Nikhilam Navataścaramam Daśataḥ, Page 14, in op. cit.
- ^ The Ūrdhva Tiryaghyām Sūtra, gives the (Ūrdhva) general formula for multiplication for each place-value. Page 41, in op. cit. Page 42, (ax+b)(cx+d) = acx² + x(ad+bc) + bd. Page 45, a vinculum (subtraction-bar) may be used on digits greater than five. Pages 49–54, the Ūrdhva-Tiryak process of multiplying for each place-value can also be applied to finding prices in aliquot parts as well as finding areas and volumes with dimensions of mixed units of measure. The converse of the Ūrdhva-Tiryak process can be used for division, both in arithmetic and with polynomials, Pages 79–83, in op. cit.
- ^ Parāvartya Yojayet, from the Parāvartya Sūtra, is a special case formula for arithmetic division and division of polynomials by Vilokanam (mere observation) by column-wise notation, Pages 64, 71, 73, 64–78, in op. cit. The use of the Ānurūpyena Sūtra (to multiply or divide the quotient proportionately to bring it closer to a power of ten) eases the calculations, pages 75–77, in op. cit.
- ^ Parāvartya Yojayet method says we can transpose terms and divide by the coefficient to solving an algebraic equation of one variable. Four general types of equations are given, pages 103–106, in op. cit.
- ^ Sūnyam Sāmyasamuccaye,pages 107–125, in op. cit. This short cut is used when solving simple algebraic equations with a certain pattern. Samuccaya is (1) Page 107, a term which is a common (variable) factor to all terms in the equation, (2) Page 107, the (variable with equal) products of the independent (constant) terms, (3) Page 108, the sum of the denominators of two fractions having the same numerator in an equation equaling zero, (4) Page 108, (with equated fractional expressions) the sum total or combination of the (binomial) numerators and denominators on both sides of the equation (and after removing any common numerical factor in that sum), (5) Page 109, (also, with equated fractional expressions that would yield a quadratic equation) the difference of the (binomial) numerator and denominator on each side (where the sum and the difference give both roots), and (6) (with a sum of fractional expressions on each side of the equation having the same numerator) the sum total of the denominators. Page 112–113, sometimes, in cases 5 and 6 above, if a variable coefficients ratios test is passed, the Parāvartya method (to divide the N by the D, converting the numerators to unity, and transpose fractional expressions as needed) can be applied to simplify the fractions, then look for Samuccaya. Pages 114–115, cross-multiplication test. Pages 116–123, cross-addition test for cubic and biquadratic fractional expressions with binomials in arithmetic progression Pages 126–139, by Parāvartya method and Samuccaya, the merger of fractional expressions algorithm. Here, the RHS fractional expression whose denominator is a first degree binomial can be merger with the sum of fractional expressions on the LHS. Pages 127–128, a general proof, p/(x+a) + q/(x+b) = (p+q)/(x+c). And so, x = [bp(a-c)+aq(b-c)]/[p(c-a)+q(c-b)].
- ^ Pages 161–162, in op. cit., applying the Sūnyam Samuccaya Sūtra to solve a second special type of quadratic equation (of a fraction of binomial expressions on both the LHS and the RHS, wherein, N1 + N2 = D1 + D2). Here, the sum of the numerators (or the denominators) is set equal to zero to give the first root, and the difference of the numerator and the denominator on either side is set equal to zero to give the second root. Pages 162–163, in op. cit., Solving a third special case quadratic equation (with sums of fractional binomial expressions on both sides of the equation). One root is obtained by applying the Sūnyam Samuccaya Sūtra, and the other root is obtained by applying the Sūnyam Anyat Sūtra. Two tests must be passed before applying the Sūtras, (1) the sums of the ratios of the numerical numerator to the coefficient of the variable term in the denominator must be equal and (2) the sums of the ratios of the numerical numerator to the numerical term in the denominator must be equal. In such a case the Sūnyam Anyat formula says that one root equals zero; and the Sūnyam Samuccaya Sūtra says that D1 + D2) = 0, to give the other root on sight, by Vilokanam. Pages 164–167, in op. cit., by Sūnyam Anyat and the Paravartya Sūtra (merger technique), a fourth special case quadratic equation, where a/(x+a) + b/(x+b) = 2c/(x+c). Test of ratio of constants: a/a + b/b = 2c/c, yes, therefore, x=0. And so, by merger, (a-c)/(x+a) + (b-)/(x+b) = 0. Hence, x = (bc+ca-2ab)/(a+b-2c).
- ^ Pages 140–141, in op. cit. this is a cross-multiplication method for solving a system of two simultaneous linear equations generating a difference of cross-products for the numerator and the denominator for the value of each variable.
- ^ Pages 174–177, solving simultaneous equations with three unknowns by the Lopana-Sthāpana Sūtra, the Ānurūpya Sūtra, and the Parāvartya Sūtra. Type one contains a significant value on the RHS in only one equation, the other two equations having a zero on the RHS. From the homogeneous zero equations we derive new equations defining two of the unknowns in terms of the third. Then we substitute these values in the third equation, thereby we obtain the values of all three variables. Or we may proceed by judicious addition and subtraction of proportionate multiples to eliminate one unknown and retain the other two. Type two has significant values on the RHS in all three equations. This case can be solved by Parāvartya (cross-multiplication) thus to produce two derived equations whose RHS is zero or my addition and subtraction of judicious multiples as above.
- ^ Pages 142–143, in op. cit. Sūnyam Anyat is used to solve a special case of simultaneous linear equations when the coefficients of one variable are in ratio with the constant terms. Hence, the other variable is equal to zero.
- ^ Pages 143–144, in op. cit. Upasūtra Sankalana-Vyavakalanābhyām is used to solve a second special case of simultaneous linear equations where the x-coefficients and the y-coefficients are interchanged, immediately giving two equations with the values for (x+y) and (x-y).
- ^ We may solve cubic equations by this Pūrana-Apūrnabhayām formula with the aid of the Parāvartya Sūtra and the Lopana-Sthāpana Sūtra. When the second degree term is missing, just split the terms into (x³−1) and the remaining terms. Pages 168–170.
- ^ Pages 171–173, Applying the Pūrana method to solve fourth power equations by completing the fourth power of the binomial, (x+a)4. A special case of the sum of two fourth power binomials can be solved with a substitution. (x+m+n)4 + (x+m-n)4 = p. Let a=x+m, the average. The Vyaṣṭi Samaṣṭi Sūtra says we may use the average of middle binomial to break down the biquadratic into a simple quadratic equation (since the odd powers cancel out). Then we apply the quadratic formula. With small integral roots such an equation can be solved by inspection.
- ^ Pages 182–185, in op. cit., Calana-Kalana (Differential Calculus). The Gunaka-Samuccaya Sūtra, etc., deal with successive differentiations, Leibnitz's theorem, MacLaurin's theorem, Taylor's theorem, and the differentiation of a product (y=uv, when u and v are functions of x. Then, dy/dx = v du/dx + u dv/dx). Knowing the relation of the factors of a polynomial and successive differentials of that polynomial and with the use of the Ādyam Ādyena Sūtra (on the sum of the coefficients) one can factor polynomials, even ones with repeated factors. Page 191, in op. cit., The converse process of Integration by partial fractions.
- ^ Pages 157–159, in op. cit. Differential calculus is used in solving quadratic equations. Rule 1: In every quadratic equation in standard form, ax² + bx + c, (with a=1) the sum of its two binomial factors is equal to its first differential. Rule 2: The first differential (of each term) is obtained by multiplying the power (Dhwaja Ghāta) by the coefficient (Anka) and reducing the power by one. Rule 3: After defining the discriminant as the square of the coefficient of the middle term minus the product of double the first coefficient and double the independent (constant) term, b² – 4ac, the first differential is equal to ± the square root of the discriminant.
- ^ Sopāntyadvayamantyam, Pages 147–149, in op. cit. This Sūtra applies to solving fractional equations of a second type, when the binomial denominators are in a certain arithmetic progression, 1/AB + 1/AC = 1/AD + 1/BC.
- ^ That is, the ratio of the constant (last) terms are set equal to the fractional expression. From a corollary to Parāvartya Sūtra, Antyayoreva, Pages 149–151, in op. cit. This Sūtra applies to solving fractional equations of a third type, when the variable terms of the numerator and denominator on the left-hand side are in ratio to the entire numerator and denominator on the right-hand side, (AC+D)/(BC+E) = A/B = AC/BC = D/E. Since ABC + AE = ABC + BD, therefore, AE = BD and A/B = D/E.
- ^ Pages 151–154, in op. cit., give a fourth type of sums of special fractional expressions, where the denominators (products of binomials (or trinomials)) are in an arithmetical progression. By the Antyayoreva Sūtra, we have the sum of the series as a fraction whose numerator is the sum of the numerators in the series and whose denominator is the product of the two ends, the first and the last binomials since the middle terms drop out.
- ^ Pages 155–156, in op. cit. A fifth type of sums of special fractional expressions is where the denominators (products of binomials (or trinomials)) are in an arithmetical progression as above and the numerators are the difference of the two binomial factors in the denominator. Again, by the Antyayoreva Sūtra, we have the sum of the series as a fraction whose numerator is the sum of the numerators in the series and whose denominator is the product of the two ends, the first and the last binomials and the numerator is the difference of the first and the last term in the denominators.
- ^ Pages 186–190, in op. cit., the Parāvartya Sūtra with the relation of the numerators gives a method of separating fractional expressions into partial fractions that are ready for integral calculus.
- ^ Page 87, Vedic Mathematics when factoring quadratic expressions and in multiplying multiples and sub-multiples
- ^ Page 87, Vedic Mathematics when factoring quadratic expressions whose first coefficient is not unity
- ^ Nikhilam Sūtra, corollary one, Page 30, in op. cit. This method deals with the squaring of numbers. Page 31, (a±b)² = a² ± 2ab + b²
- ^ Nikhilam Sūtra, corollary two, Pages 33–34, in op. cit. This method deals with squaring numbers ending in five.
- ^ Nikhilam Sūtra, corollary two, sub-corollary, Antyayor-Daśake'pi, Page 34, in op. cit. Corollary two also applies to multiplying numbers whose last digits together total 10 (and other powers of ten) and whose previous part is exactly the same.
- ^ Nikhilam Sūtra, corollary three, Ekanyūnena Pūrvena, Pages 33–39, in op. cit. Pūrvena means multiplicand. This corollary applies when the Apara (multiplier) is all nines, as in some astronomical calculations. Then the multiplicand is decreased by one in the left-hand group and the right-hand group is the multiplier after being decreased by the difference of the multiplicand and one.
- ^ To factor second degree homogeneous expressions (and when finding the GCF (HCF) of polynomials, page 98) we use the Ādyamādyena Sūtra (the first by the first and the last by the last, page 87) and the Lopana-Sthāpana sub-sūtra, Page 90, in op. cit.
- ^ Pages 159–161, in op. cit., Solving the special quadratic equations of the form of the sum (or difference) of reciprocals by the Vilokanam sub-sūtra. When the LHS is x ± 1/x, merely split the RHS constant into reciprocals, a/b ± b/a. Both solutions are then obvious. a/b ± b/a = (a² ± b²)/ab. Page 296, in op. cit., the sum or difference of squares formula, (a+b)² – (a-b)² = 4ab, where a and b are the factors of a number.
- ^ Pages 178–181, in op. cit. When the x and y values are symmetrical and one equation is xy = a constant, then one set of solutions of certain simultaneous quadratic equations can be done by Vilokanam. Once the value of x or y has been found, having the value of the xy-term at once gives the value of the other variable. The reversal of signs gives the other set of values. The techniques for solving linear systems of equations, (1) factoring and substituting or (2) careful multiplications and addition (or subtraction) can eliminate a variable in many other cases.
- ^ Pages 1, 1a, Vedic Mathematics
- ^ Page 89, Vedic Mathematics
- ^ Pages 14–39, in op. cit.
- ^ Page 30, in op. cit.
- ^ Page 31, in op. cit.
- ^ Tim Guest (2004-01-09). "A breath of fresh air from India". Times Educational Supplement. http://www.tes.co.uk/article.aspx?storycode=389051. Retrieved 2010-08-26.
- ^ World Academy of Science, Engineering & Technology - journal
- ^ Academy & Industry Research Collaboration Center - journal
- ^ IETE - journal
- ^ Cornell university library
References
- Agrawala, V. S. (1992). General editor's note. Vedic mathematics (pp. v-viii)Motilal Banarsidass Publishers Private Limited.
- Dutta, . (2002). Mathematics in Ancient India. Seattle, Wash.: Resonance Media.
- Gaskell, M. (2000). Try a sūtra. The Times Educational Supplement, , M10.
- Glover, J. (2002, Vedic Mathematics Today (Only a Matter of 16 Sutras). Education Times.
- Kansara, N. M. (2000). Vedic sources of the Vedic mathematics. Sambodhi Vol. XXIII.[1]
- Pratyagatmananda, S. (1965). Forward. Vedic mathematics (pp. ix-xii). Delhi: Motilal Banarsidass Publishers Private Limited.
- Tirthaji, Bharati Krsna Maharaja. (1992). In Agrawala V. S. (Ed.), Vedic mathematics. Delhi: Motilal Banarsidass Publishers Private Limited.
- Trivedi, S. M. (1965). My beloved gurudeva. Vedic mathematics (pp. xxiii). Delhi: Motilal Banarsidass Publishers Private Limited.
- Veda. In L. L. Bram, & N. H. Dickey (Eds.), Funk and Wagnalls New Encyclopedia (pp. 417–418). Funk and Wagnalls L.P.
- Williams, K. (2000). The sūtras of Vedic mathematics. Baroda: Oriental Institute.
- Dr.C.Nagalakshmi,(2010), Vedic Mathematics (Easy Methods in Mathematics),Emesco Books, Hyderabad